|
|
||||||||||||||||
|
||||||||||||||||
|
Vigenère Ver und Entschlüsselung
History and a small Tool to demonstrate the Vigenère en- and decypherment.
Downloads and Links Erläuterung 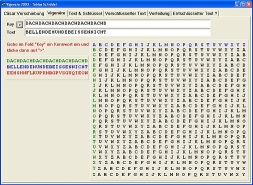 
Kurzbeschreibung:Die Vigenère Verschlüsselung basiert auf einer modifizierten Cesar-Verschiebung. Jeder Buchstabe des Originaltextes wird durch den um n verschobenen Buchstaben des Alphabetes substituiert. Entgegen der Cesar-Verschiebung ist n hierbei jedoch nicht für alle Zeichen identisch. Vielmehr macht es die permanente Veränderung von n unmöglich die Häufigkeitsanalyse der Buchstaben in einem Text als Werkzeug zur Dechiffrierung zu verwenden.Historie:Blaise de Vigenère (*1523) entwickelte 1549 aufbauend auf die von Alberti, Trithemius und Porta um 1460 niedergeschriebene Abhandlung über den Einsatz mehr als eines Geheimtextalphabetes beim Substitutionsverfahren die sog. Vigenère Verschlüsselung. Er schaffte es, eine ausgereifte und starke Verschlüsselung zu spezifizieren, da er einen Weg fand, die von Alberti willkürlich zusammengestellten Geheimalphabete mittels einer Matrix und eines Codeworts abzulösen. Erst dadurch wurde das Problem gelöst, dass der gewünschte Adressat der Nachricht nur einen vergleichsweise kurzen Schlüssel benötigte und nicht mehrere "durchgewürfelte" Alphabete als auch die jeweilige Verschiebung kennen und aufbewahren musste.
Geknackt wurde die Vigenère Verschlüsselung durch Charles Babbage (*1791) um etwa 1854. Angeregt durch den Patentantrag des Zahnarztes John Hall Brook Thwaites, der eine Verschlüsselungsmethode "erfunden" hatte ohne zu wissen, dass diese exakt der rund zweihundert Jahre alten Vigenère Verschlüsselung entsprach. Babbage, der als Auditor den Patentantrag ablehnte, erhielt kurze Zeit später einen verschlüsselten Brief des Zahnarztes aus Bristol in dem dieser Babbage aufrief, den Text zu knacken.
Charles Babbage erfand und entdeckte im Laufe seines Lebens weitere, heute noch genutzte Dinge wie den Tachometer, den Kuhschieber (vorne an alten Dampflokomotiven), das Einheitsporto, eine Sterblichkeitsanalyse aber auch einen frühen, mechanischen Computer. Da Babbage seine Methode zum Knacken der Verschlüsselung nie veröffentlichte sondern diese erst nach seinem Tod gefunden wurde, schreibt man ihm die Lösung im nachhinein als Erstem zu. Die erste Veröffentlichung machte aber unabhängig von Babbages Erkenntnissen der preussische Major a.D. Friedrich Wilhelm Kasiski in seinem Buch "Geheimschriften und die Dechiffrir-Kunst". Verschlüsselung:Für diese Beschreibung wählen wir den Satz "Bellende Hunde beissen nicht" um ihn zu verschlüsseln. Dazu werden Satzzeichen und Leerzeichen zwischen den Wörtern entfernt. Aus lesbarkeitsgründen wird hier eine rein in Großbuchstaben dargestellte Schreibweise verwendet (BELLENDEHUNDEBEISSENNICHT). Der Chiffrierer wählt nun ein Schlüsselwort. Wir verwenden das Wort DACH in unserem Beispiel. Das Schlüsselwort wird nun sooft konkatiniert, bis es die Länge des zu verschlüsselnden Textes hat. BELLENDEHUNDEBEISSENNICHT hat 25 Buchstaben. Dazu muss das Schlüsselwort DACH (4 Buchstaben) 7 mal konkatiniert werden, wobei die letzte drei Buchstaben unnötig sind und abgeschnitten werden können. Wir verwenden also DACHDACHDACHDACHDACHDACHD. Nun wird jeder n-te (1 bis 25) Buchstabe des Originaltextes mit dem n-ten Buchstaben des verlängerten Codewortes veschlüsselt. Die Verschlüsselung ist eine Substitution um x Stellen, wobei x die Position des n-ten Buchstaben des Codeworts im Alphabet (beginnend bei Null) ist. DACHDACHDACHDACHDACHDACHD BELLENDEHUNDEBEISSENNICHT Der erste Buchstabe. B wird mit D verschlüsselt. D ist der 4 Buchstabe im Alphabet. Da die Zählung bei Null (A=0, B=1, C=2, etc) beginnt, wird B um drei Stellen im Alphabet verschoben, sodass der erste verschlüsselte Buchstabe ein E wird. Dieses Vorgehen wird nun für alle weiteren 24 Buchstaben wiederholt. D A C H D A C
H D A C H D A C H D A C H D A C H D B E L L E N D E H U N D
E B E I S S E N N I C H T E E N S H N F L K U P K H B G P V S G U Q I E O W Um die Ver- und Entschlüsselung zu vereinfachen kann eine Matrix verwendet werden, die die jeweils verschobenen Alphabete darstellt. Das Ergebnis der Verschlüsselung eines Buchstaben ist dabei der Schnittpunkt der horizontalen Reihe und vertikalen Reihe ist. Die horizontale Reihe wird so gewählt, dass der erste Buchstabe gleich dem Buchstaben des Codewortes ist. Die vertikale Reihe so, dass der erste Buchstabe gleich dem zu verschlüsselnden Buchstaben des Originaltextes ist.
Entschlüsselung:Die Entschlüsselung des Textes ist recht einfach und auch ohne Computer zu machen, sofern das Codewort bekannt ist. Die Vorgehensweise bei der Verschlüsselung mit der Matrix wird einfach umgedreht. Ist dieses nicht bekannt, war es bis Charles Babbage für viele Jahrzehnte eine sichere und unknackbare Methode. Selbst die Häufigkeitsanalyse der Buchstaben, mit der der arabische Gelehrte al-Kindi die monoalphabetische Substitution, die auch der Cesar Verschiebung zugrunde liegt, knacken konnte hilft hier erst einmal nicht weiter. Auch wenn es noch mehrere Versuche und verschiedene andere Lösungsansätze gab, so konnte eine
Vigenère Verschlüsselung nur mit ausreichend "Material" - sprich relativ langen Texten - geknackt werden.
War der Text sehr kurz - zum Beispiel nur drei bis vier paar Worte lang - bissen sich auch die besten Kryptographen die Zähne aus.
Der Grund liegt in der Verwendung des Codewortes (DACH). Zwar ist klar, dass hier jeder vierte (DACH ist vier Zeichen lang) Buchstabe mit der gleichen Verschiebung verschlüsselt wurde, jedoch ist dieses Wissen zumindest wenig hilfreich, solange die Länge des Codewortes nicht bekannt ist. Je länger das Codewort ist um mehr ähnelt die Verschlüsselung der Nutzung eines One-Time-Pad, welches ja bekanntlich unknackbar ist. Würde man jedoch die Länge des Codewortes kennen, ist es möglich den verschlüsselten Text zu stückeln und in einzelne Töpfe stecken. Auf jeden Topf kann nun die einfache Häufigkeitsanalyse (siehe weiter unten) angewandt werden. Bei derart kurzen Texten wie in unserem Beispiel wird aber auch das nichts nützen. Ebenso tragen derart kurze Texte nicht dazu bei, die Länge des Codewortes zu erraten - dem ersten Schritt um die Vigenère Verschlüsselung zu knacken. Der Grund liegt in der Tatsache, dass uns auch hier die Häufigkeitsanalyse hilft, jedoch nicht von einzelnen Buchstaben, sondern von Buchstabenpaaren. Babbage entdeckte, dass in einem Klartext Buchstabenpaare
wie z.B. "ER" oder "UM" häufiger vorkommen als z.B. "IO" oder "PK". Die
Wahrscheinlichkeit, dass in einem langen Text diese Buchstabenpaare bei der Verschlüsselung
nach Vigenère unter der gleichen Stelle des
Codewortes liegen ausreichend hoch. In solchen Fällen wird zwangsweise auch der
verschlüsselte Text identisch sein. Suchen wir also nach mehrfach vorkommenden Buchstabenkombinationen
im verschlüsselten Text (nehmen wir einen anderen, nämlich LNWSPUPKXMWSPHGYXM 123456789012345678 LNWSPUPKXMWSPHGYXM XM kommt zweimal vor und zwar an den an den Positionen 9 und 17. Doch selbst dieser kurze Text hat noch mehr zu bieten. Wir finden zusätzlich noch ein wiederkehrendes dreistelliges Buchstabenpaar. 123456789012345678 LNWSPUPKXMWSPHGYXM
WSP kommt ebenso zweimal vor. Wir finden es an den Positionen 3 und 11. Buchstabenkombinationen aus mehr als zwei Buchstaben erhöhen die Wahrscheinlichkeit eines Treffers. Wir werden gleich sehen, warum dies so ist. Gehen wir davon aus, dass unsere Buchstabenpärchen wirklich mit den jeweils gleichen Buchstabenpärchen des Codewortes verschlüsselt wurden. Da das Codewort mit der Länge n konkatiniert wurde, muss jeder n-te, jeder n+1-te, jeder n+2-te usw Buchstabe gleich verschlüsselt sein. Demnach müssten unsere Buchstabenpärchen einen Abstand haben, der durch n teilbar wäre. XM kommt an den Positionen 9 und 17 vor. Die Differenz von 17-9 ist 8. WSP kommt an den Positionen 11 und 3 vor. Auch hier ergibt sich eine Differenz von 8. 8 ist ganzzahlig teilbar durch 1, 2, 4 und 8. Schliessen wir ein- und zweistellige Passwörter aus, können wir davon ausgehen, dass das Codewort 4 oder 8 Stellen lang ist.
Beispiel für ein
sechsstelliges Codewort Natürlich muss nicht jedes gleiche verschlüsselte Buchstabenpärchen mit den gleichen Buchstaben des Codewortes veschlüsselt worden sein. Die Buchstabenkombination kann auch anders zustande kommen. Dies ist aber eher unwahrscheinlich, also zufällig der Fall. Hier helfen uns mehrere unterschiedliche Buchstabenpärchen dabei, diese Ausreisser zu identifizieren und auszuschliessen. Durch dieses Ausschlussverfahren kommen wir schliesslich auf die Länge des Codwortes. In unserem Beispiel hat es vier Stellen. Wir zerstückeln also Bei einem Codewort mit vier Zeichen Länge werden vier Töpfe benötigt, in die wir die jeweiligen n-ten, n+1-ten, n+2-ten und n+3-ten Buchstaben des verschlüsselten Textes geben. 1234 1234 1234 1234
12 LNWS PUPK XMWS PHGY
XM Topf 1: L P X P X Topf 2: N U M H M Topf 3: W P W G Topf 4: S K S Y Auf jeden Topf kommt nun die Wahrscheinlichkeitsanalyse zur Anwendung. Grundlage dieser Entschlüsselungsmethode ist die Kenntnis der verwendeten Sprache. In deutschen Texten ist das "E" der häufigste Buchstabe. Zählt man alle Buchstaben in Texten z.B. aus Romanen oder Zeitungsartikeln erhält man eine Verteilungswahrscheinlichkeit der aller Buchstaben.
Nun erstellen wir eine Verteilungsstatistik für jeden unserer vier Töpfe und vergleichen sie mit der natürlichen Verteilung. Bei ausreichend langen Texten werden sich die Statistiken sehr ähneln, die Balken sind nur verschoben.
Die Grafik zeigt eine Verschiebung um 4 Stellen. Die untere Verteilung
zeigt Topf n, womit der n-te Buchstabe
des Codewortes ein "D" wäre. Analog verfahren wir mit allen Töpfen
und kommen dadurch auf das Codewort DACH. Bei unserem Beispiel LNWSPUPKXMWSPHGYXM haben wir also das
Codewort DACH
verwendet. Unter Anwendung der gleichen Matrix, die beim Verschlüsseln angewendet wurde können wir den Text nun entschlüsseln. DACHDACHDACHDACHDA LNWSPUPKXMWSPHGYXM INULMUNDUMULMHERUM Der Klartext lautet "In Ulm und um Ulm herum". Anmerkung:Diese Verschlüsselungsmethode wurde leicht abgewandelt bis etwa 1998 für Textdokumente in Star*Office verwendet. Download "Vigenère Demo"Autor: Tobias Schrödel Februar 2005 | |||||||||||||||











